|
This week's newsletter has been translated into Spanish by Ed Campos, Jr. Make sure you check it out and tell him thank you on Twitter. The link to share is bit.ly/TTMspanish43 Edmund Harriss, author of Visions of the Universe, stopped by to talk about a seemingly simple idea that gets more complex every time we think about it. How does addition work, anyways? Come find out! How many additions can you find with the same answer? A good part of mathematics begins with counting, which can be thought of as just adding 1 several times to get each whole number in turn. The next step is to add in, addition. This is just repeated counting, beginning a pattern of repeated operations that we could explore in all sorts of ways, but instead we shall pause here and see what can be done with just addition. The next paragraph breaks down the exploration into occasionally agonising detail, but has lots of additional questions to dig even deeper. From counting, we already have one way to get each number:
2 = 1+1 3=1+1+1 4=1+1+1+1 and so on If instead we combine some of the additions at each stage, we get some new ways: 3=2+1 4=3+1 5=4+1 and so on How else could we make four? 2+2 springs to mind, so just looking at 4 we now have 3 different ways to make it: 1+1+1+1 3+1 2+2 keeping just 2 numbers 1+3 is another possibility Do we consider that the same as 1+3? Are there other ways? We have 1+1+1+1 which is the sum of four numbers, unless we allow 0 which would create all sorts of problems (why?) we cannot make any of the numbers to add smaller, so this is the only option. We also have 3+1, 2+2 and possibly 1+3 with two numbers. We could have 4 for just a single number. So with 1,2 and 4 we are missing 3. We can 2+1+1 as a way to add three, depending on your answer to the question of 3+1 and 1+3 this might be the only option, or you might also have 1+2+1 and 1+1+2 (why are there not other options?). This gives a complete list of possibilities for 4. Exploring 4 above, you notice that the emphasis is on the questions more than the answers. For one thing, we are looking at all the addition questions that give a certain answer 4, the opposite of the first experience of mathematics. In addition, the question of whether 1+3 and 3+1 are the same does not have a right answer, but the answer given has consequences later. That answer gives two different answers to the motivating question "How many ways can you add to 4?". If we allow re-orderings to be different then there are eight, if we say they are the same then there are still five different ways. Now think about a larger number, say 5. Can you write a list of all ways to make that? With some written down, challenge each other to make more, until you cannot find any more. You can also discuss how to count the number of ways to count orders. For example 1+1+2 has three orders as we saw above, but 1+2+3 to make 6 can be put into six different orders (can you find them?). For larger numbers still, you might want to try to find systems that give all options. For example if you choose 11, that can be made in 56 different ways (even not counting reorders). A good way to explore all options is with a dot pattern like this one for 4 (how these relate to the 5 ways of adding is left as a puzzle), these are called Young or Ferrers diagrams and have applications in a variety of places in mathematics and physics. You can see all the diagrams for 11 in my colouring book Visions of the Universe (Visions of Numberland in the UK), along with a lot of other visual mathematics to play with.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Details
AuthorJohn Stevens is working to give parents ideas on how to have mathematics-based discussion at home. Archives
May 2018
Categories |

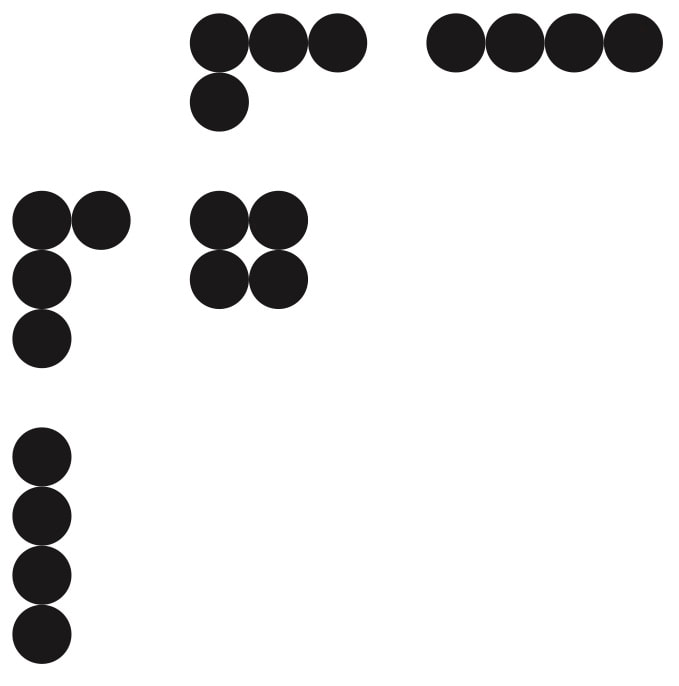
 RSS Feed
RSS Feed