|
The image above was shared with me on Instagram (wait, you didn't know I started an Instagram account?! Check it out now!) by Ben Cogswell and the caption he included was one I just had to share (with his permission, of course):
Waiting for lunch discussing what makes this number special? 9 year old: use fractions to make this number. 7 year old: make this number with 3 addends. 4 year old: Make 7 on your fingers then make 10! I love it. With such an open prompt and one that was literally placed onto his table, Ben and his kids engaged in an appropriately-leveled task with each one of his kids. All are at different stages of their numeracy journey, yet they all were able to access the prompt he put forth. And yes, for those asking, Ben was sent a fresh signed copy of Table Talk Math :) When doing this with my students, I would put the "day" value of the date onto the whiteboard and have students come up with as many interesting expressions that equal that number in 60 seconds. For example, if today were August 10th, the number on the board would be 10 and I might get: (11+9) * 5 - 90 10 + 0 ...and a bunch of others The point here is that I am giving you the solution and you are being tasked with giving me the problem. No matter how old your child is, this is an idea you can use and it's also a great way to pass the time as you're waiting for that meal out as a family. Try it out! Ben isn't the only one getting a signed copy of the book; take a picture of the number, along with the problem and your child's work to prove that it's correct, and I'll pick one reply to get a signed copy of Table Talk Math. It's that easy! Things to encourage:
If--WHEN--there are incorrect answers, leave them until all expressions have been shared. Then, when everyone has had a turn, come back to the incorrect one and ask to go through it together. "Now that we have done this and realize that it isn't quite 17, what can we do to the existing problem to make it true?" By going in and correcting your child's work, you are making it less inviting to try again. On the contrary, building on top of the work that you notice together provides an opportunity to fix an incorrect response and make it more complex than original. This naturally empowers the child to try again and gives you a good basis of conversation. Try it out! What number did you show to your child (or your child show to you) and what expressions did you come up with? Reply to this email, Tweet it out to me, or share it on Facebook and tag Table Talk Math. Thanks for joining the Table! If you have any questions, please feel free to contact me on Twitter (@TableTalkMath) or comment below. Be sure to have your friends sign up for the newsletter at tabletalkmath.com for weekly updates. Thank you for taking the time to improve math fluency for children, one table talk conversation at a time.
0 Comments
If you have read Table Talk Math, you know how much I loved playing games as a kid and how much I love them now. That is why this week's newsletter, written by Daniel Finkel, resonated to much. Check out what he has to share about Tiny Polka Dot and get your set today: To help kids ____, we ____ with our kids. There’s a question floating around in the background when people talk about how to help young kids get off to a good start with math. We know what to do with reading, after all! To help our kids read, we read to our kids. What’s the math version? To help our kids math, we math to our kids? It just doesn’t have the right ring. It’s precisely because we are not clear what math means as a verb that this is so hard. There are a range of suggestions on what nurturing this mathematical instinct in young children looks like, including some, like Bedtime Math, that take the analogy with bedtime stories very literally. And I’m thrilled these ideas are out there! The good news is that children naturally are drawn to counting, and they won’t learn to dislike math unless someone teachers them to. But how do we help them have the opportunity to love math? For me, the answer was games. I played countless hours of Sorry, Rummy, Casino, Yahtzee, Hearts, Backgammon, and so on when I was younger. Cribbage, especially, was a popular game in my house. My brothers and I played endlessly, and I learned, as all cribbage players must, all the ways to make fifteen. To this day, I can casually glance at a hand of 6 cards and instantly tell you how many fifteens are in there. It’s a skill developed through hours of play, and one that made school math in Kindergarten through 2nd grade nearly effortless. So that’s my answer to fill in the blanks: To help kids love math, we play math with our kids. As I’ve understood more about how counting, logic, and reasoning develop, I’ve come to see virtually all card and board games as contributing to mathematical growth. Abstract logic games like chess, checkers, hex, go, Connect 4, and so on help build the critical “what if” creative/logical muscle in the mind. “If I go here, what will my opponent do?” I love these games, and there are plenty of great ones. But what about games to help with numbers, counting and arithmetic specifically? The games that exist in this capacity tend to have an academic feel, and play can be subordinate to “learning.” Young kids come to understand numbers through a surprisingly complex process that takes years. Fortunately, playing and counting and exploring their way through this process can be a pleasure, as long as they are unhurried. Kinesthetic work with blocks and other objects is critical, but games can be harder to find. We wanted to provide a rich structure to explore how numbers work and relate. Essentially, we wanted to make a deck of cards that would allow all the play I’d had as a child, but that made the mathematical and counting connections even richer and more fun. That’s why we built Tiny Polka Dot. It’s a mathematically enriched card deck with 16 games you can play with very young (3 year old) to older (8 and up) kids. There’s a ton of research that went into this game, but I think the most compelling case for its value is the fun kids have playing it, and how they engage with math and counting as they go. Setting up Hungry Numbers (more videos at tinypolkadot.com/learn-to-play) One fascinating thing about the deck is that it has all the versatility of an actual deck of cards, albeit one with 6 suits from 0 to 10. I haven’t played Tiny Polka Dot cribbage yet, but I want to. Meanwhile, I keep hearing about innovations and child-created games. For example, this older student invented her own take on the Polka Loop Puzzle that blew me away. And this, to me, is where play leads: to perseverance and ownership and curiosity and creativity; to pushing beyond the bounds of the puzzle into something new, for no other reason than it’s fun to explore. When we talk about learning to love math, this is what we’re talking about: not mere “mastery,” but ownership - the understanding that it belongs to you, and you can break it and put it back together again because it’s yours. That’s where play leads.
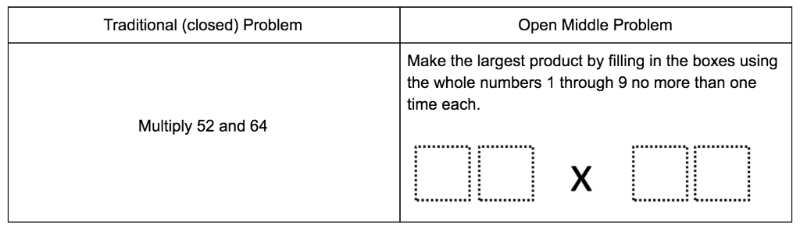
To help kids learn math, know math, and love math, we play math with our kids. Thanks for joining the Table! If you have any questions, please feel free to contact me on Twitter (@TableTalkMath) or comment below. Be sure to have your friends sign up for the newsletter at tabletalkmath.com for weekly updates. Thank you for taking the time to improve math fluency for children, one table talk conversation at a time. Rather than telling you about it myself, I've brought in Nanette Johnson, the co-creator of a phenomenal resource called Open Middle. Here is what she has to say: Having kids of my own, I have a 10, 8 and 7 year old, I like when they explain their reasoning, especially in math. One of the challenges that parents may have is helping their child explain their reasoning. I have found some success by asking questions. One of my favorite questions to ask my own kids is, “Can you think of a different way to get the same answer?” This helps them know that math, along with other things, has more than one way to get to the solution. Another reason I love this question is that it helps them validate their answer using a different method. If they get the same answer using 2 seemingly unrelated methods, this gives them confidence in their answer. First, let’s define what an Open Middle problem is. Imagine that a problem has a beginning (the problem or question), a middle (solution path) and an end (the answer or solution). Most problems from a textbook have closed beginning, closed middle and closed end - meaning, they all start, continue and end the same exact way. Instead, Open Middle problems are different in that, they have an open middle, meaning that there are multiple ways to get to the solution. These multiple ways allow students to approach the problem in different ways to validate their answer. Knowing various ways to arrive at the same solution and knowing how these methods are connected strengthens your child’s math skills. So here is an analogy to help better explain this. Imagine that you are at home, but need to go to somewhere (maybe the store or a friend’s house). Are there multiple ways to get there? If you said yes, that’s an example of something having an open middle. You have the same beginning and end, but the middle has different options. Consider these two problems: The traditional problem doesn’t offer much variation, especially in the middle, unless you prompt your student.
The Open Middle problem asks the student to find the LARGEST product. Once they get an answer, ask questions such as:
Another difference between these two problems is the level of complexity in thinking that each is asking of the student. The first problem is likely something their teacher may have shown them how to do. The second is asking something that they most likely have never been asked, but they have the ability to do (given that he/she has learned multiplication). You can help your child become a stronger mathematician not by asking them to do something (or variations of the something) they have seen and done before, but by giving them tasks that are different than what they’ve done before, yet have the ability to complete. So, how can you turn Open Middle Problems into Table Talks? Choose a problem from OpenMiddle.com. The site is organized by grade level, but I strongly suggest a problem that is two or three grade levels below (just to get them used to this kind of thinking). Also, begin with a lower DOK (depth of knowledge, which indicates the level of complexity of thinking required to complete the problem). Do the problem before you give it to them and read any hints or answers that your kid may need. Ask your kids to do the problem (or show them the problem). If your child gets stuck, start asking questions to help guide their thinking to get to the answer. Here are a some of questions that you can use:
Thanks for joining the Table! If you have any questions, please feel free to contact me on Twitter (@TableTalkMath) or comment below. Be sure to have your friends sign up for the newsletter at tabletalkmath.com for weekly updates. Thank you for taking the time to improve math fluency for children, one table talk conversation at a time. When is 100 + 100 NOT equal to 200?
I'm about to challenge everything you have ever thought about addition. After all, it's one of the absolutes in the world: 2 + 2 = 4 10 + 11 = 21 and... 100 + 100 = 50? Every week, I would give my students a challenge on the side board; a brain teaser, a puzzle, or an interesting math problem. The ones that got the most traction were the number puzzles like the ones I'm sharing in this week's newsletter. The only hint I will give you is that this whole activity is a conversation starters for why the proper units matter. With that said, I'll open the challenge up to you:
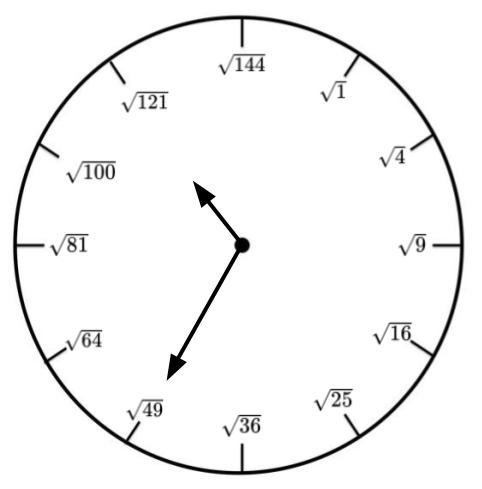
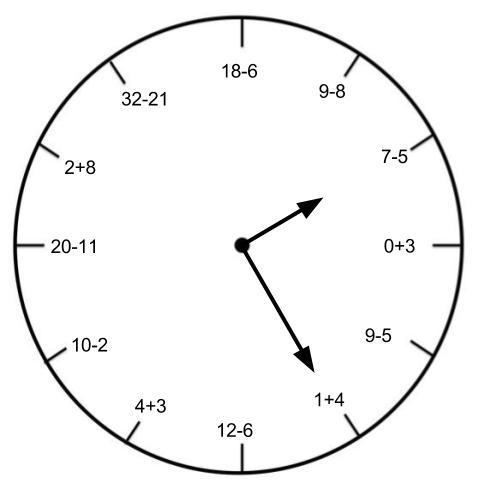
Here they are!!! When does 100 + 100 = 50? When does 100 + 100 = 3 1/3? When does 100 + 100 = 60.96? When does 100 + 100 = 1.5625? As a bonus, come up with one of your own and send it my way to see if my boys and I can figure it out! Thanks for joining the Table! If you have any questions, please feel free to contact me on Twitter (@TableTalkMath) or comment below. Be sure to have your friends sign up for the newsletter at tabletalkmath.com for weekly updates. Thank you for taking the time to improve math fluency for children, one table talk conversation at a time. What Time Is It? This week's newsletter has been translated into Spanish by Ed Campos, Jr. Make sure you check it out (http://bit.ly/TTMspanish47) and tell him thank you on Twitter. Clocks are too helpful. Sure, they're supposed to tell time and everything, but it's just too easy to see what time it is. I'm thinking that we try something like this. What time is it? If you're used to looking at an analog clock, you know right away that it is 11:35 based on the clock above. However, if you aren't, there are a few things in play. First, you need to know the square roots. Each of the numbers 1-12 have been replaced by the square roots of their perfect squares, and this is great practice for kids who are learning about them. Second, you need to know which hand is the hours (the small hand) and which hand is the minutes (the large hand). Teaching kids to know the difference between the two will certainly help! Third, you need to know that the hours count as advertised and the minutes count their value times 5. Therefore, the square root of 49 is 7, then 7 times 5 is 35, meaning that the minute value of the time is 35. While these things may seem trivial to you as an adult (maybe), there is a lot of decoding happening with a clock and kids. Because of that, this is not an activity I would recommend with kids who are barely learning how to read a clock. For example, this is a lesson I used with my 8th grade students as a review of square roots, and could be used much earlier. Maybe that was too tough. Try this one with your elementary-aged child: Did you get 2:05? 12:20? 2:20? Something else?
How? Once your child gets the hang of clockwork, it will be time for you to lay out some new challenges. Click here for a template that you can use for your own ideas. Print it, make a copy of it in your Google Drive, open it on a writeable tablet... or maybe there's something else you can do. And when you do, I want to see what you come up with. Take a picture and email it to me by dropping a comment below. I am thrilled to have Chris Shore take over the newsletter this week to share about his experiences with Clotheslines. This week's newsletter has been translated into Spanish (bit.ly/TTMspanish46) by Ed Campos, Jr. Make sure you check it out and tell him thank you on Twitter. From Chris: A person’s ability to think mathematically has far more to do with their number sense than with their ability to study and memorize formulas and procedures. Number sense is the capacity to think flexibly, efficiently, and accurately about numbers. One of the great methods in teaching number sense is the open number line, which is a number line with no or few given benchmarks. I’m currently working extensively with this open number line concept using an instructional tool know as the Clothesline. The Clothesline is a dynamic number line (string) on which students can actually move the values and benchmark (folded cards). For example, let’s say we ask students to place the following three fractions: 1/2, 1/3, 1/4 Typically, students will use only 0 and 1 as benchmarks, then many will often inaccurately place the fractions in the following order: This misconception offers a great opportunity to discuss how when something is divided into more and more equal parts, each part gets small. For example, 1/2 of a pizza is a bigger slice than 1/4 of the same size pizza. Once the order of the fractions is correct, students are prompted to properly space the fractions. While students frequently find the proper spacing for one-half and one-fourth, one-third challenges them. Is it closer to the fourth or the half? There are several strategies for determining this, from converting to decimals (0.25, 0.33..., 0.50), finding a common denominator (3/12, 4/12, 6/12) or proportional reasoning (three thirds equals exactly one). As a parent at home working with the number line with your child, you don't need to try to do the teacher’s job. Simply share aloud how you think about these numbers. We math teachers call these “number talks,” and it is one of the most effective ways you can support your child’s learning of mathematics.
If you are interested playing with the Clothesline or simply the open number line on paper, you can find free resources on clotheslinemath.com First, I must say thank you to Kent Haines and Christopher Danielson for posting prompts like these on Twitter recently. This week's newsletter has been translated into Spanish by Ed Campos, Jr. Make sure you check it out and tell him thank you on Twitter. Quick! Look at the image above and tell me how many eggs you see in the crate! This is not only a fun prompt to try at home, it's also a great insight into how you group objects to count them more efficiently. Did you count the first long row, the second row with the individual egg on one side and the pair on the other, then move the third row and finish it off? Did you start with the fact that there egg crates hold 12 eggs, then subtract out the missing ones? Did you approach it differently? More importantly, how did your child approach it and did that differ from yours? How about this one? Was it easier to count these? More difficult? Our brains work in mysterious and interesting ways. For me, I'm taking the group of four, group of two, and group of four, then combining them all. Do you see it? I love bringing my kids to the counter and challenging them with these quick prompts, none of which take a lot of creativity and offer a lot of opportunity for thoughtful responses. That is, until you go and start cracking eggs: How many eggs do you see? What qualifies? How did you count?
This week's newsletter has been translated into Spanish by Ed Campos, Jr. Make sure you check it out and tell him thank you on Twitter. The link to share is bit.ly/TTMspanish44
Matt Lane, author of Power-Up: Unlocking the Hidden Mathematics in Video Games, grabbed ahold of the newsletter control board to talk about video games. Why would I want my kids to play video games? Is there value in them? Read below to find out. With school out for summer, you've likely already made plans to keep your kids active, engaged in learning, and off of the couch. But if your kids are anything like me when I was a kid, they'd rather stay at home and play video games. Fortunately, there are opportunities for rich mathematical conversations that arise from these games, even the ones that aren't expressly designed to be educational. Here are three reasons why it's worth engaging your kids in video games, especially when it comes to mathematics: 1. They're relevant. According to the Entertainment Software Association's 2017 report, Essential Facts About the Computer and Video Game Industry, 65% of households in the US have at least one person who plays video games for at least three hours per week. It's a multibillion dollar industry that already appeals to millions of people, kids included. 2. They have pedagogical value. In his 2011 book Mathematics Education for a New Era: Video Games as a Medium for Learning, mathematician Keith Devlin argues for using video games not only to teach basic arithmetic and numeracy, but also to help foster a a productive disposition, which the National Research Council defines as "A habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one's own efficacy." 3. They have a precedent. Did you know that Tetris has been linked to one of the Clay Mathematics Institute's Millenium Prize problems? Or that the origins of probability theory can be traced to a series of letters between mathematicians Pierre de Fermat and Blaise Pascal about a parlor game? Here's a simplified version of what they discussed (it's now known as The Problem of Points) Suppose you and your child are playing a game where you both have an equal chance of winning each round. The first to win a certain number of rounds (say, 4) wins a prize. If the game is interrupted before either player can reach 4 wins, how should the price be fairly divided? To put it in concrete terms, what if you are winning 3 games to 1 when the game is interrupted? What if you're only winning 2 games to 1? If you're looking to spark some interesting mathematical conversation, the Problem of Points is a great place to start. And if you'd like explore the intersection between math an video games in more detail, consider checking out my new book! It's called Power-Up: Unlocking the Hidden Mathematics in Video Games. Also, here are some recommended games to play with your kids, along with their ratings: Threes! (4+) Portal 2 (E10+) The Witness (E) Fez (E) The Sims 4 (T) Enjoy your summer! And if you ever want to chat more about math or video games, you can find me on Twitter (@mmmaaatttttt - that's matt cubed). This week's newsletter has been translated into Spanish by Ed Campos, Jr. Make sure you check it out and tell him thank you on Twitter. The link to share is bit.ly/TTMspanish43 Edmund Harriss, author of Visions of the Universe, stopped by to talk about a seemingly simple idea that gets more complex every time we think about it. How does addition work, anyways? Come find out! How many additions can you find with the same answer? A good part of mathematics begins with counting, which can be thought of as just adding 1 several times to get each whole number in turn. The next step is to add in, addition. This is just repeated counting, beginning a pattern of repeated operations that we could explore in all sorts of ways, but instead we shall pause here and see what can be done with just addition. The next paragraph breaks down the exploration into occasionally agonising detail, but has lots of additional questions to dig even deeper. From counting, we already have one way to get each number:
2 = 1+1 3=1+1+1 4=1+1+1+1 and so on If instead we combine some of the additions at each stage, we get some new ways: 3=2+1 4=3+1 5=4+1 and so on How else could we make four? 2+2 springs to mind, so just looking at 4 we now have 3 different ways to make it: 1+1+1+1 3+1 2+2 keeping just 2 numbers 1+3 is another possibility Do we consider that the same as 1+3? Are there other ways? We have 1+1+1+1 which is the sum of four numbers, unless we allow 0 which would create all sorts of problems (why?) we cannot make any of the numbers to add smaller, so this is the only option. We also have 3+1, 2+2 and possibly 1+3 with two numbers. We could have 4 for just a single number. So with 1,2 and 4 we are missing 3. We can 2+1+1 as a way to add three, depending on your answer to the question of 3+1 and 1+3 this might be the only option, or you might also have 1+2+1 and 1+1+2 (why are there not other options?). This gives a complete list of possibilities for 4. Exploring 4 above, you notice that the emphasis is on the questions more than the answers. For one thing, we are looking at all the addition questions that give a certain answer 4, the opposite of the first experience of mathematics. In addition, the question of whether 1+3 and 3+1 are the same does not have a right answer, but the answer given has consequences later. That answer gives two different answers to the motivating question "How many ways can you add to 4?". If we allow re-orderings to be different then there are eight, if we say they are the same then there are still five different ways. Now think about a larger number, say 5. Can you write a list of all ways to make that? With some written down, challenge each other to make more, until you cannot find any more. You can also discuss how to count the number of ways to count orders. For example 1+1+2 has three orders as we saw above, but 1+2+3 to make 6 can be put into six different orders (can you find them?). For larger numbers still, you might want to try to find systems that give all options. For example if you choose 11, that can be made in 56 different ways (even not counting reorders). A good way to explore all options is with a dot pattern like this one for 4 (how these relate to the 5 ways of adding is left as a puzzle), these are called Young or Ferrers diagrams and have applications in a variety of places in mathematics and physics. You can see all the diagrams for 11 in my colouring book Visions of the Universe (Visions of Numberland in the UK), along with a lot of other visual mathematics to play with. This week's newsletter has been translated into Spanish by Ed Campos, Jr. Make sure you check it out and tell him thank you on Twitter. The link to share is bit.ly/TTMspanish42
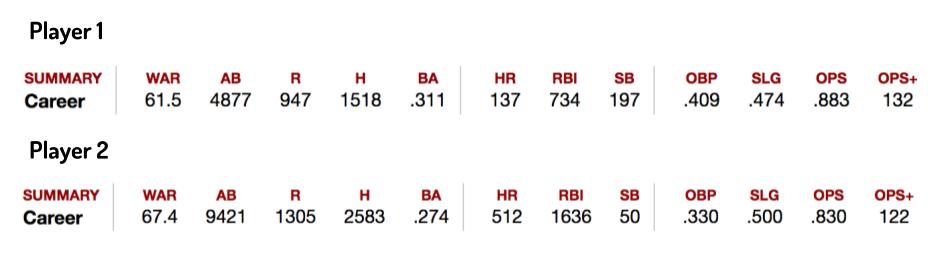
Based solely on the career statistics lines that you see above, would you rather have Player 1 or Player 2 on your team? I intentionally took off the names so you could only rely on statistics. Which ones are the most important to you when looking to build a team? Player 1 only had 137 home runs and 734 runs batted in, yet he had a .409 on base percentage. On top of that, he had almost half the at bats as Player 2, leading us to believe that he played for about half as many seasons. Meanwhile, Player 2 only stole 50 bases and had a much lower batting average, yet he hit far more home runs and had substantially more runs batted in. For more context, and in honor of this being the 42nd newsletter, Player 1 is the stat line of Jackie Robinson, the man famous for breaking Major League Baseball's color barrier. Not only did he put up this impressive career line of stats, he did so while breaking into the league when African American athletes were not welcomed--or allowed--on the same field as their white counterparts. He was the Rookie of the Year during his rookie season and also earned an MVP award. His number, 42, is the only number to be retired across all of baseball. Player 2 is the stat line of Ernie Banks, a Hall of Fame player who spent 19 seasons with the Chicago Cubs. Banks came into the league just a few seasons after Robinson and endured many of the same issues. While he took second place in the Rookie of the Year voting, he did manage to earn two MVPs for this performances. Now that you have this information, does it change your decision? Which player do you go with and what is your mathematical justification? Maybe you and your child(ren) aren't into baseball, and that's just fine. Here are some other sports that might interest you at the table: WNBA basketball NBA basketball NHL hockey NFL football Premier League soccer NASCAR racing Right now is a great time to be a fan of sports, with finals here and seasons in full swing. If you sit down to enjoy the game, turn it into a learning opportunity as well! |
Details
AuthorJohn Stevens is working to give parents ideas on how to have mathematics-based discussion at home. Archives
May 2018
Categories |




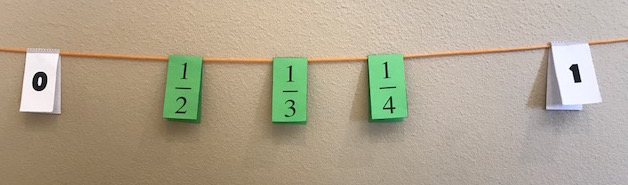
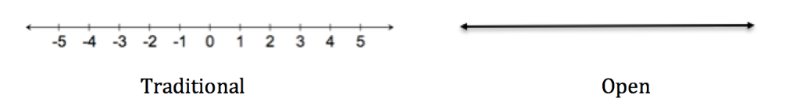
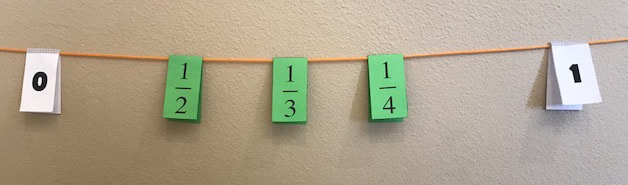
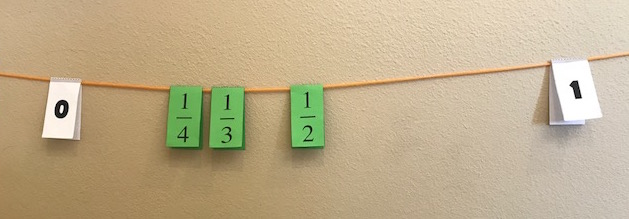




 RSS Feed
RSS Feed